1.1 Función de dos variables
Una función de dos variables es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y sólo un número real z.
El conjunto de parejas ordenadas para las cuales la regla de correspondencia da un número real se llama dominio de la función. El conjunto de valores z que corresponden a los pares ordenados se llama imagen o contra-dominio.
Una función de dos variables se denota usualmente con la notación:
z = f (x, y)
Las variables x, y se llaman variables independientes, y z se llama variable dependiente.
La gráfica de una función de dos variables es el conjunto de puntos con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).

En consecuencia, la gráfica de una función f de dos variables es una superficie que consta de todos los puntos del espacio tridimensional cuyas coordenadas cartesianas están determinadas por las ternas ordenadas de números reales (x, y, z). Como el dominio de f es un conjunto de puntos del plano x, y, y puesto que cada par ordenado (x, y) del dominio de f corresponde a solo un valor de z, ninguna recta perpendicular al plano x,y puede interceptar a la gráfica de f en mas de un punto.
1.2 Derivadas Parciales.
En matemática, una derivada parcial de una función de diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en cálculo vectorial y geometría diferencial.
La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:
Donde  es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
 es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
Cuando una magnitud  es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,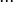 ), es decir:
), es decir:
 es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,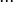 ), es decir:
), es decir:
Supongamos que 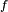 es una función de más de una variable, es decir una función real de variable vectorial. Para el caso,
es una función de más de una variable, es decir una función real de variable vectorial. Para el caso,
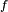 es una función de más de una variable, es decir una función real de variable vectorial. Para el caso,
es una función de más de una variable, es decir una función real de variable vectorial. Para el caso,
Es difícil describir la derivada de tal función, ya que existe un número infinito de líneas tangentes en cada punto de su superficie. La derivación parcial es el acto de elegir una de esas líneas y encontrar su pendiente. Generalmente, las líneas que más interesan son aquellas que son paralelas al eje x, y aquellas que son paralelas al eje y.
1.3 Máximos y mínimos de funciones de dos variables.
1.4 Aplicaciones: Optimización de funciones de dos variables que representen gastos, ingresos o utilidad.
Función de Costo
Una función costo especifica el costo C como una función de la cantidad de artículos x. En consecuencia, C(x) es el costo de x artículos, y tiene la forma
Costo = Costo variable + Costo fijo
en la que el costo variable es una función de x y el costo fijo es constante. Una función costo de la forma
C(x) = mx + b
se llama una función costo lineal; el costo variable es mx y el costo fijo es b.La pendiente m, el costo marginal, mide el costo incremental por artículo.
Función de ingreso
El ingreso que resulta de una o más transacciones comerciales es el pago total recibido, y a veces se la llama ingreso bruto. Si I(x) es el ingreso por vender x artículos al precio de m cada uno, entonces I es la función lineal I(x) = mx y el precio de venta m se puede tamién llamar ingreso marginal.
Ejemplo
Suponga que su casa editorial vende libros ciencia ficción rústicos a una detallisa para $6.50 por libro. Entonces
I(x) = 6.50x dolares.
El ingreso marginal es m = $6.50 por libro.
Función utilidad
La utilidad es el ingreso neto, o lo que queda de los ingresos después de restar los costos. Si la utilidad depende linealmente en el número de artículos, entonces la pendiente m se llama la utilidad marginal. La utilidad, el ingreso, y el costo son relacionados por la siguiente formula:
Utilidad = Ingreso − Costo
U = I − C
Si la utilidad es negativa, por ejemplo −$500, se denomina pérdida (de $500 en este caso). El equilibrio, salir a la par o salir tablas quiere decir no obtener utilidades ni tener pérdidas. De esta forma, equilibrio ocurre cuando U = 0, o
I = C Equilibrio
El puno equilibrio es el número de articulos x a lo cual presenta el equilibrio.
Ejemplo
Si regresamos al ejemplo de las novelas ciencia ficción, ya tenemos las funciones costo y ingreso:
C(x) = 3.50x + 1200 dollars. Costo diario de imprimir x libros
I(x) = 6.50x dollars. Ingresos por la venta de x libros
Conclusión: Las funciones son más simples pero aplicando la fórmula son complejas.
Conclusión: Las funciones son más simples pero aplicando la fórmula son complejas.
Bibliografía:
Matemáticas para
administración y economía Haeusler Pearson/ Prentice Hall, 10° Edición, 2008.

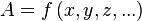
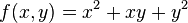
No hay comentarios.:
Publicar un comentario